注：该系列是我在学习《数据结构与算法之美》课程时，为加深理解和日后翻看所做的笔记及个人思考的记录。

复杂度分析

事后统计法

将代码跑一遍，测试得到算法的执行时间和占用内存的空间大小这种事后统计法虽然是正确的，但是有很大的局限性：

测试结果非常依赖测试环境
测试结果受数据规模影响很大

大O复杂度表示法

时间复杂度

1	T(n) = O(f(n))

T(n) 表示代码的执行时间，n 表示数据规模的大小，f(n) 表示每行代码执行的次数总和，上面的公式就表示所有代码的执行时间与每行代码的执行次数成正比。

大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是代表代码执行时间随数据规模增长的变化趋势，所以也叫渐进时间复杂度。当 n 很大时，f(n)中的低阶，常量，系数并不左右增长趋势，所以可以忽略，只记录一个最大量级就可以了。例如：T(n)=O(n²)，T(n)=O(logn)这样。常见的时间复杂度有如下几种：

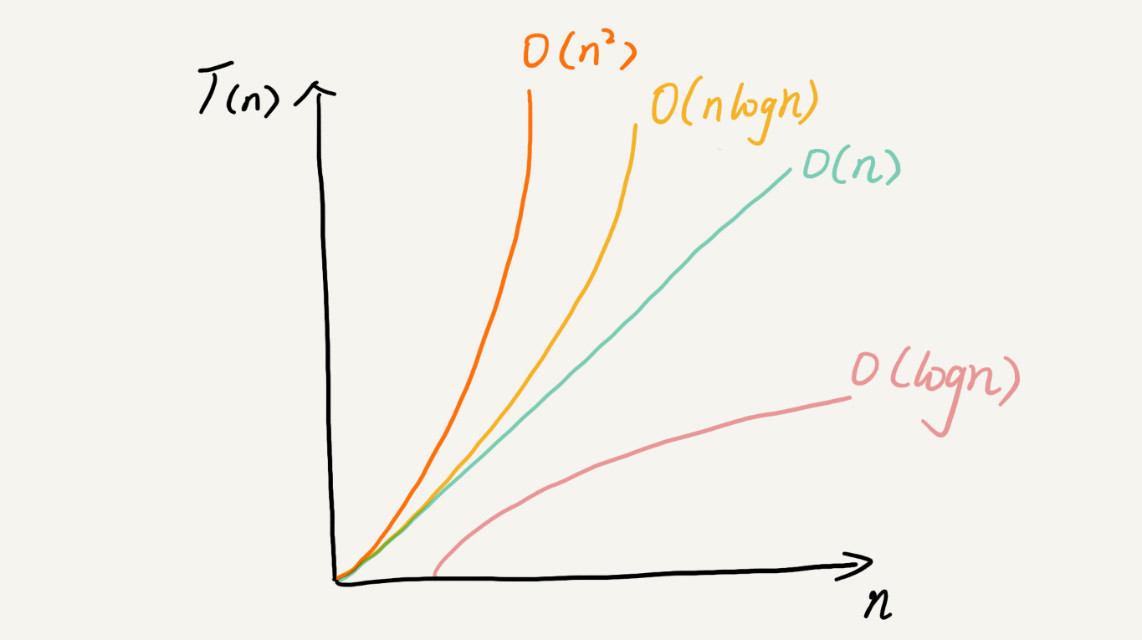
最好/最坏情况时间复杂度：是指在最理想/最糟糕的情况下，执行这段代码的时间复杂度。
平均时间复杂度：最好/最坏时间复杂度对应的都是极端情况下的复杂度，平均复杂度将各种情况发生的概率考虑进去，是所有情况下代码执行次数的加权平均值。
均摊时间复杂度：均摊时间复杂度其实是一种特殊的平均时间复杂度，一般是指对一个数据结构进行一组连续操作中，大部分情况下时间复杂度都很低，只有个别情况下时间复杂度较高，而且这些操作之间存在前后连贯的时序关系，此时，我们将这一组操作放在一起分析，看能否将较高时间复杂度的那次操作的耗时均摊到其他时间复杂度比较低的操作上。

空间复杂度

表示算法的存储空间与数据规模增长的变化趋势，也叫渐进空间复杂度。

数组

数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。

线性表是一种数据排成一条线一样的结构，每个线性表上的数据最多只有前和后两个方向。数组、链表、队列、栈都是线性表结构。

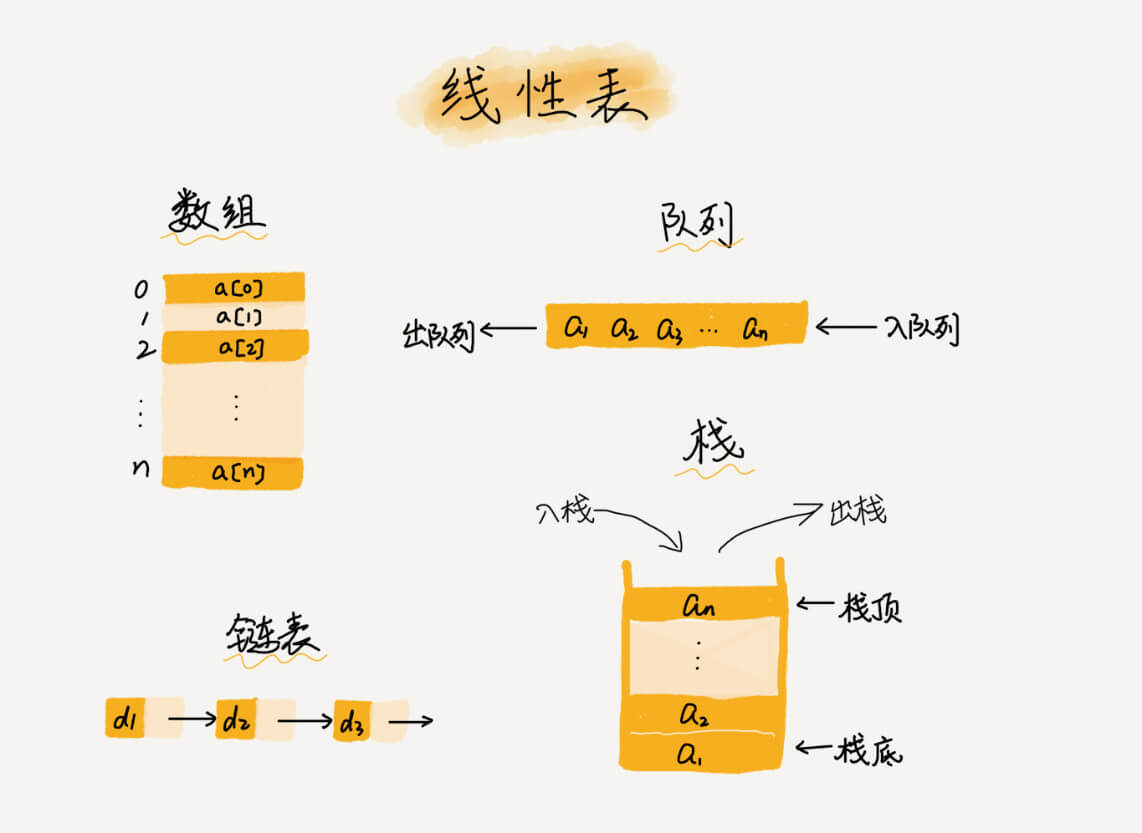
在非线性表中，数据之间并不是简单的前后关系。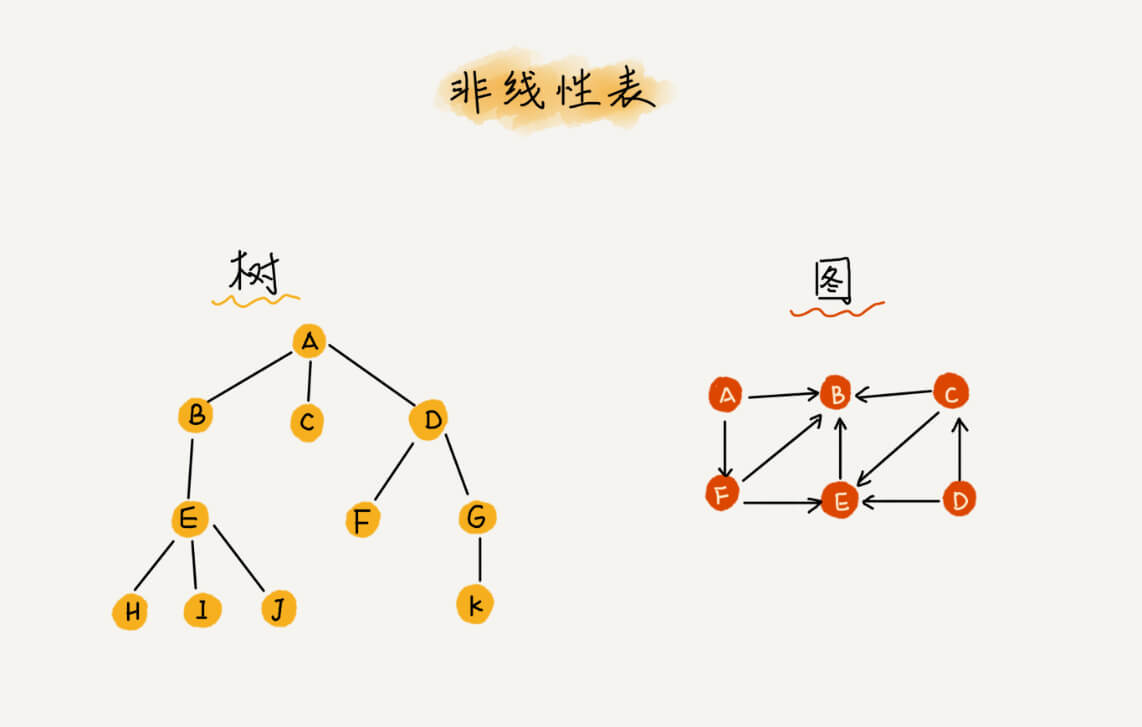

连续的内存空间和相同类型的数据使得数组支持根据下标随机访问的特性。

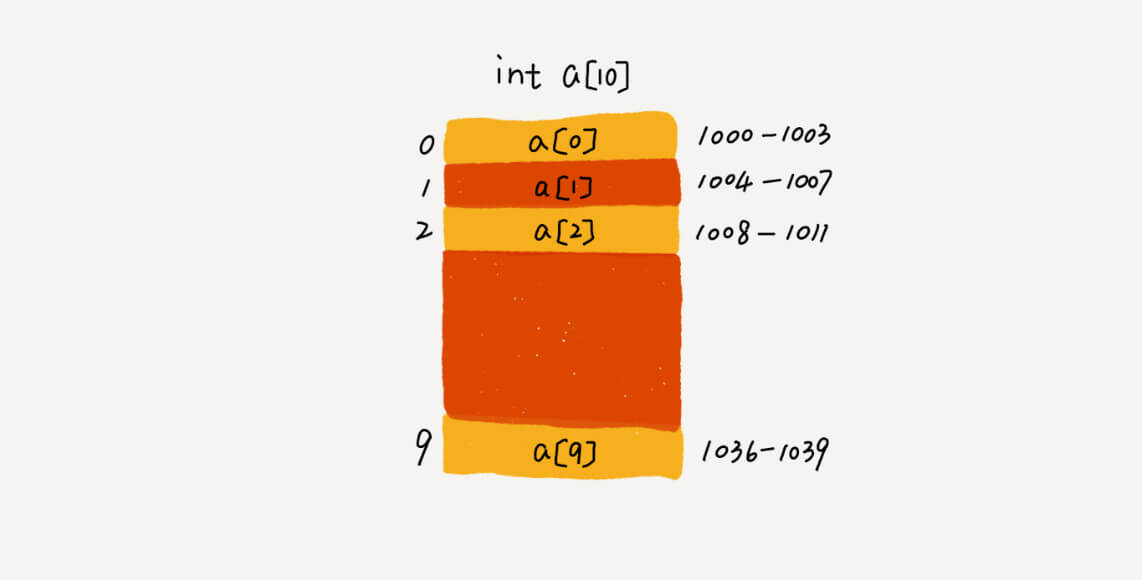
1 2	//按下标随机访问数组中某个元素时，通过如下寻址公式，计算出该元素的内存地址 a[i]_address = base_address + i * data_type_size

插入操作：将一个数据插入到长度为 n 的数组的第 k 个位置，需要先将 k~n 的这部分元素顺序向后挪一位，再插入新元素。其最好、最坏及平均时间复杂度为 O(1)、O(n)、O(n)。但是当数组中的数据没有任何规律，只是被当做存储数据的集合时，可以直接将第 k 位数据搬到数组的最后，将新元素直接放到第 k 位，将时间复杂度减为 O(1)。
删除操作：与插入操作类似，为保证内存连续性，也需要搬移数据。最好、最坏及平均时间复杂度也为 O(1)、O(n)、O(n)。但是在某些特殊情况下，我们不追求数据的连续性时，可以采取标记元素已经被删除，并不真正搬移数据，只有在数组没有更多的存储空间时才执行一次真正的删除操作，这样大大减少了操作导致的数据搬移。

数组越界问题

在 C 语言中，只要不是访问受限的内存，所有的内存空间都是可以自由访问的。数组越界在 C 语言中是一种未决行为，并没有规定数组访问越界是时编译器应该如何处理。因为访问数组的本质就是访问一段内存地址，只要数组通过偏移计算得到的内存地址是可用的，那么程序就不会报错。

链表

与数组不同，链表并不需要一块连续的内存，它通过“指针”将一组零散的内存块串联起来使用。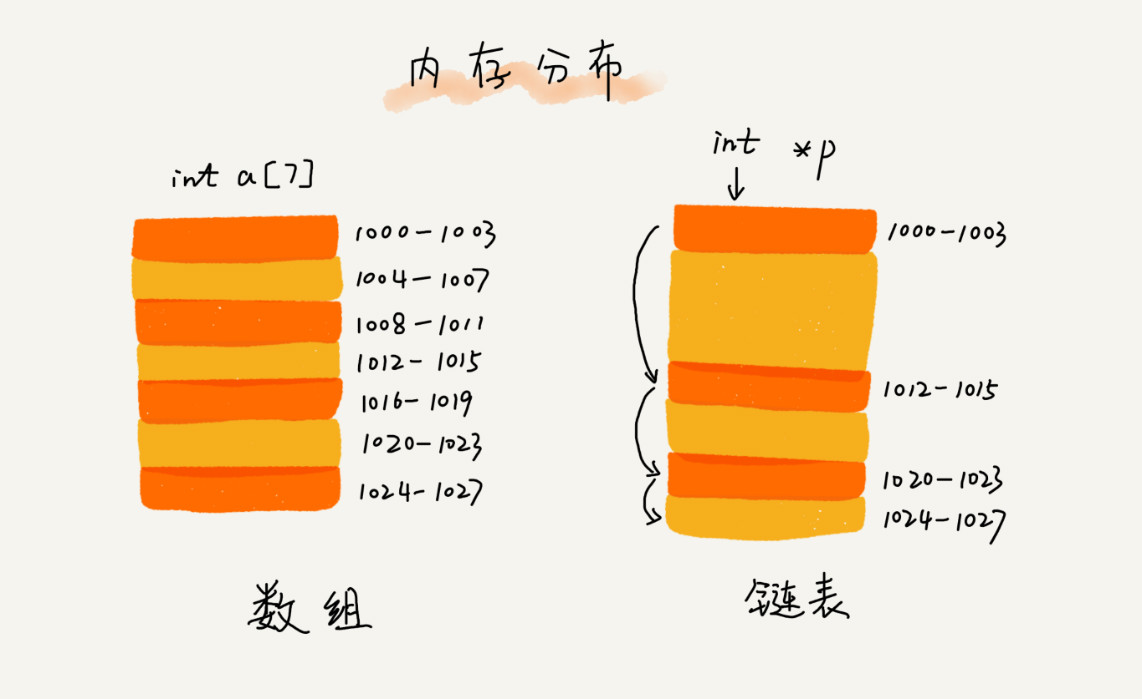

单链表

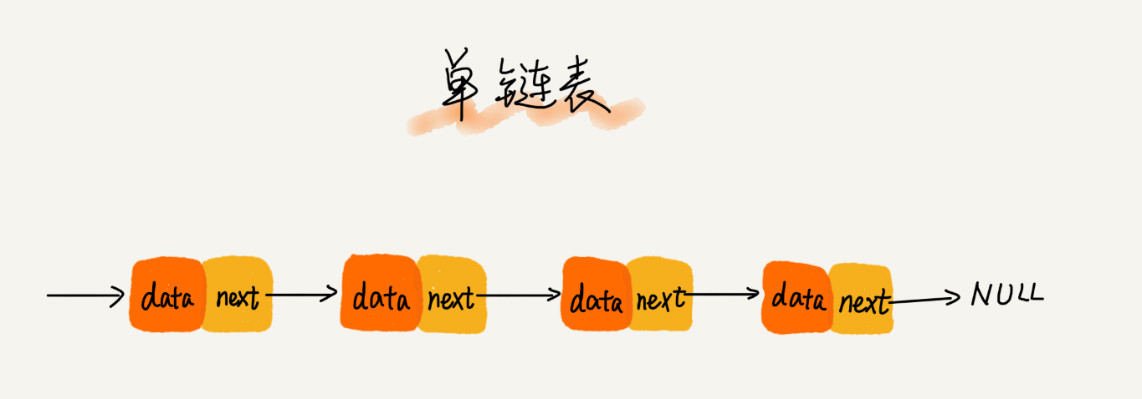
链表的插入删除操作只需要考虑相邻结点的指针改变，因此时间复杂度为 O(1)，但是想要随机访问第 K 个元素就需要顺着指针依次遍历了，时间复杂度为 O(n)。

循环链表

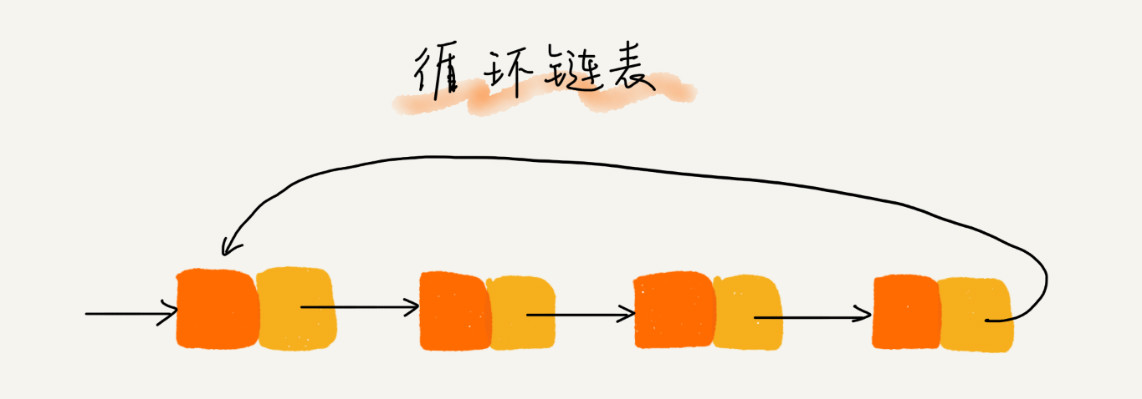
双向链表

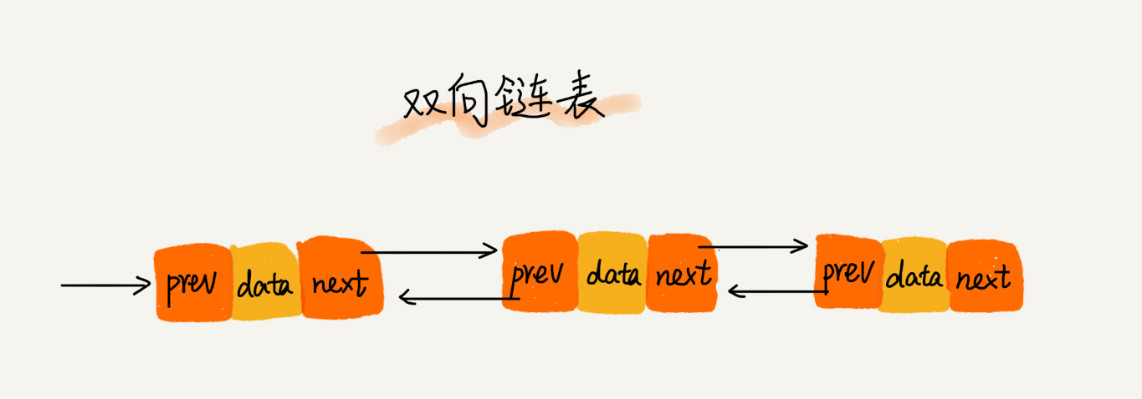
如何基于链表实现 LRU 缓存淘汰算法

我们维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时，我们从链表头开始顺序遍历链表：

如果该数据已经被缓存在链表中了，我们遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部。
如果此数据没有缓存到链表中，若此时缓存未满则将此结点直接插入到链表的头部，若此时链表已满则删除链表尾结点，将新的数据结点插入到链表头部。

写好链表代码的技巧

将某个变量赋值给指针，实际上就是将这个变量的地址赋值给指针，或者反过来说，指针中存储了这个变量的内存地址，指向了这个变量，通过指针就能找到这个变量。
对于非自动内存管理的语言来说，删除链表结点时，也一定要记得手动释放内存。
为简化编程逻辑，可以引入哨兵结点，这样不管链表是不是空，head 指针都会一直指向这个哨兵结点，这种有哨兵结点的链表叫带头链表。

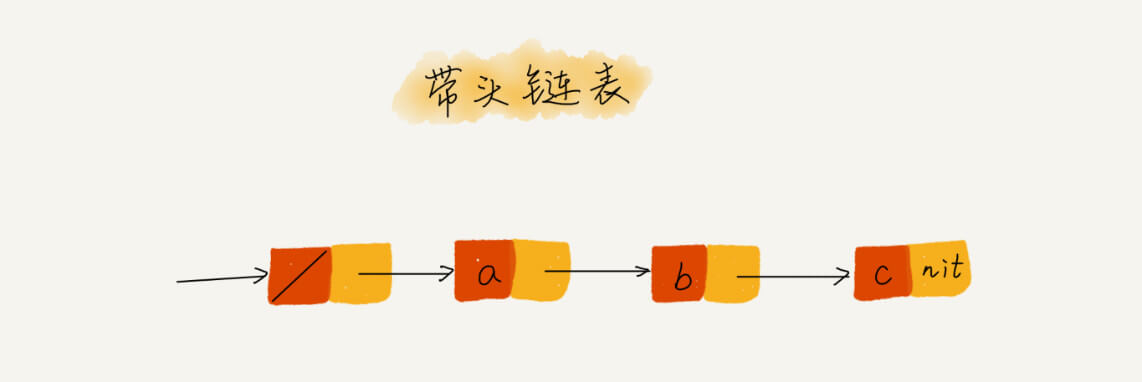
重点留意边界情况，如链表为空时，链表只有一个结点时，链表头结点跟尾结点的操作等等。

栈

栈是一直“操作受限”的线性表，只允许在一端插入和删除数据，并且满足后进先出，先进后出的特性。栈只支持两个基本操作：入栈 push()和出栈 pop()。

栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈，我们叫作顺序栈，用链表实现的栈，我们叫作链式栈。

栈在函数调用中的应用

操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。

栈在表达式求值中的应用

编译器是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。我们从左向右遍历表达式，当遇到数字，我们就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较。如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。

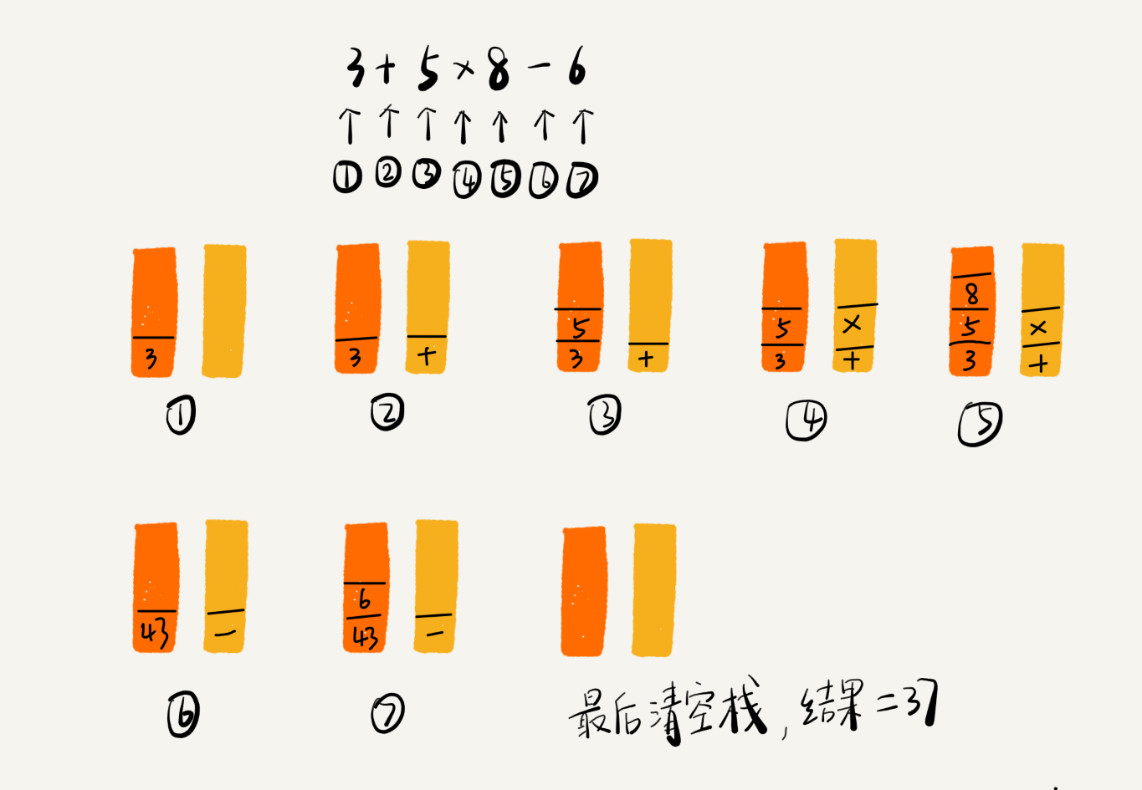
栈在括号匹配中的应用

假设表达式中只包含三种括号，圆括号 ()、方括号 [] 和花括号{}，并且它们可以任意嵌套。比如，{[{}]}或 [{()}([])] 等都为合法格式，而{[}()] 或 [({)] 为不合法的格式。我们用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。

队列

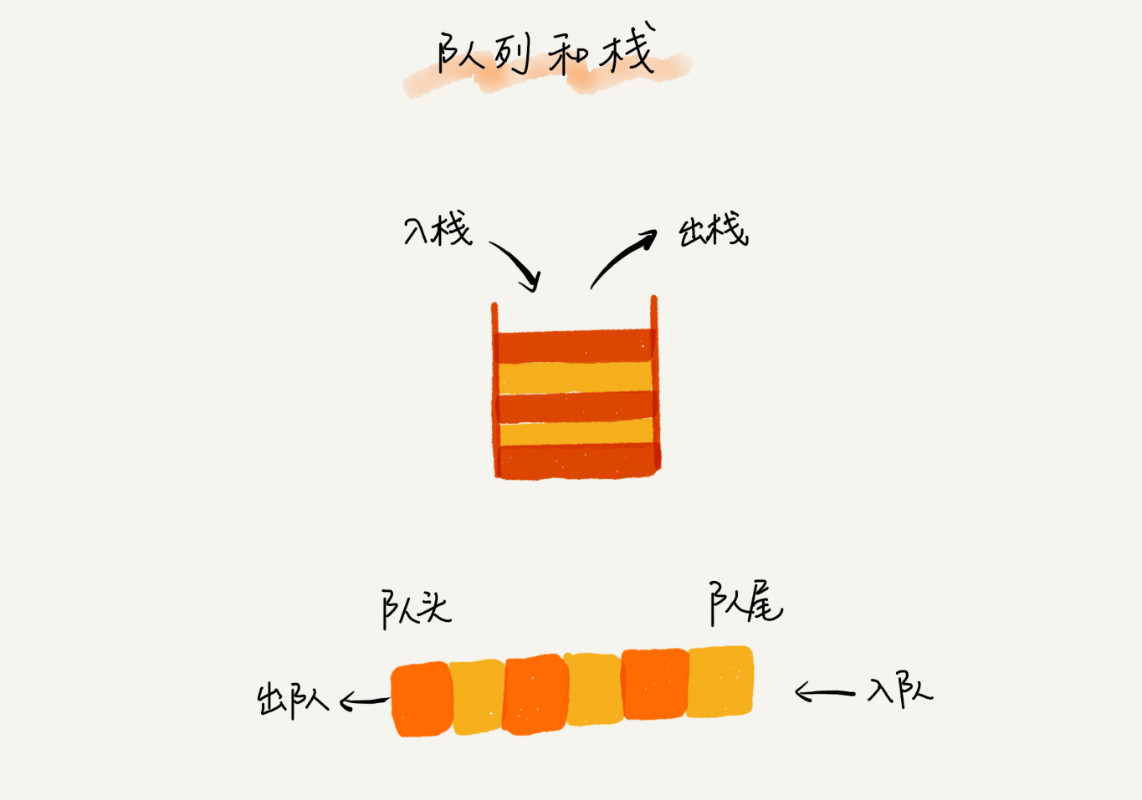
队列跟栈一样，也是一种操作受限的线性表数据结构。它满足先进先出的特性，最基本的操作也是两个：入队 enqueue()，放一个数据到队列尾部；出队 dequeue()，从队列头部取一个元素。

跟栈一样，队列可以用数组来实现，也可以用链表来实现。用数组实现的队列叫作顺序队列，用链表实现的队列叫作链式队列。

循环队列

循环队列是为了解决在顺序队列中入队当 tail=n 时的数据搬移的问题。

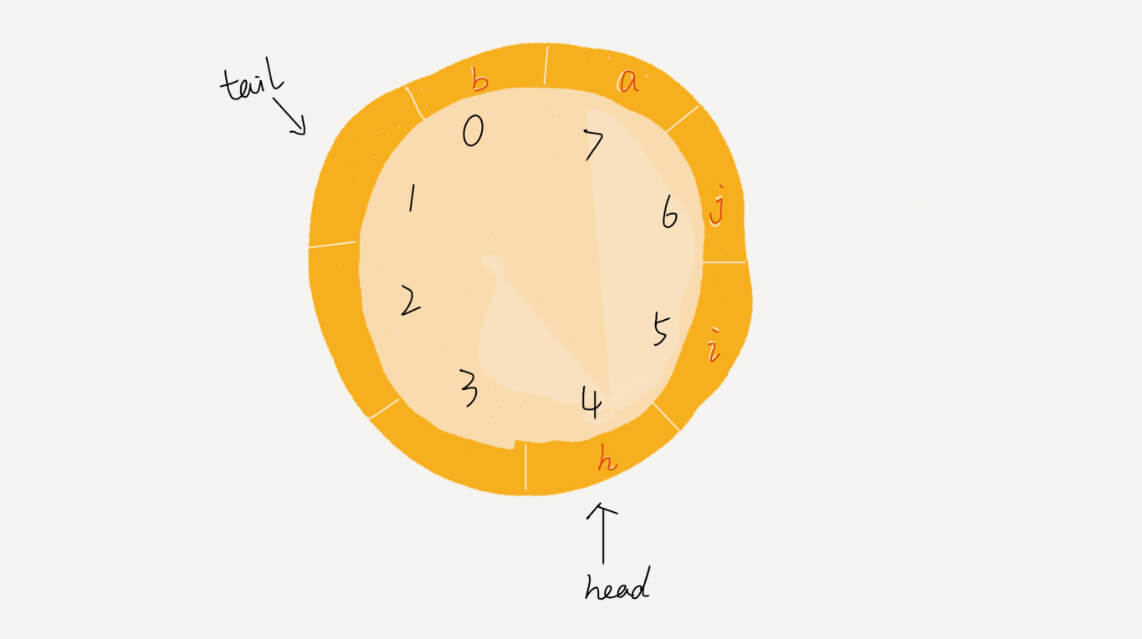
使用循环队列最关键的问题是确定好队空和队满的判定条件。在用数组实现的非循环队列中，队空的判断条件是 head == tail，队满的判断条件是 tail == n。在循环队列中队空的判断条件仍然是 head == tail，判断队满的条件为 (tail+1)%n=head。

递归

递归需要满足的三个条件

一个问题的解可以分解为几个子问题的解
这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
存在递归终止条件

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

Deep Thought

《数据结构与算法之美》笔记-线性表数据结构