Deep Thought
0%

《数据结构与算法之美》笔记-排序

发表于 更新于 分类于

排序比较

冒泡排序

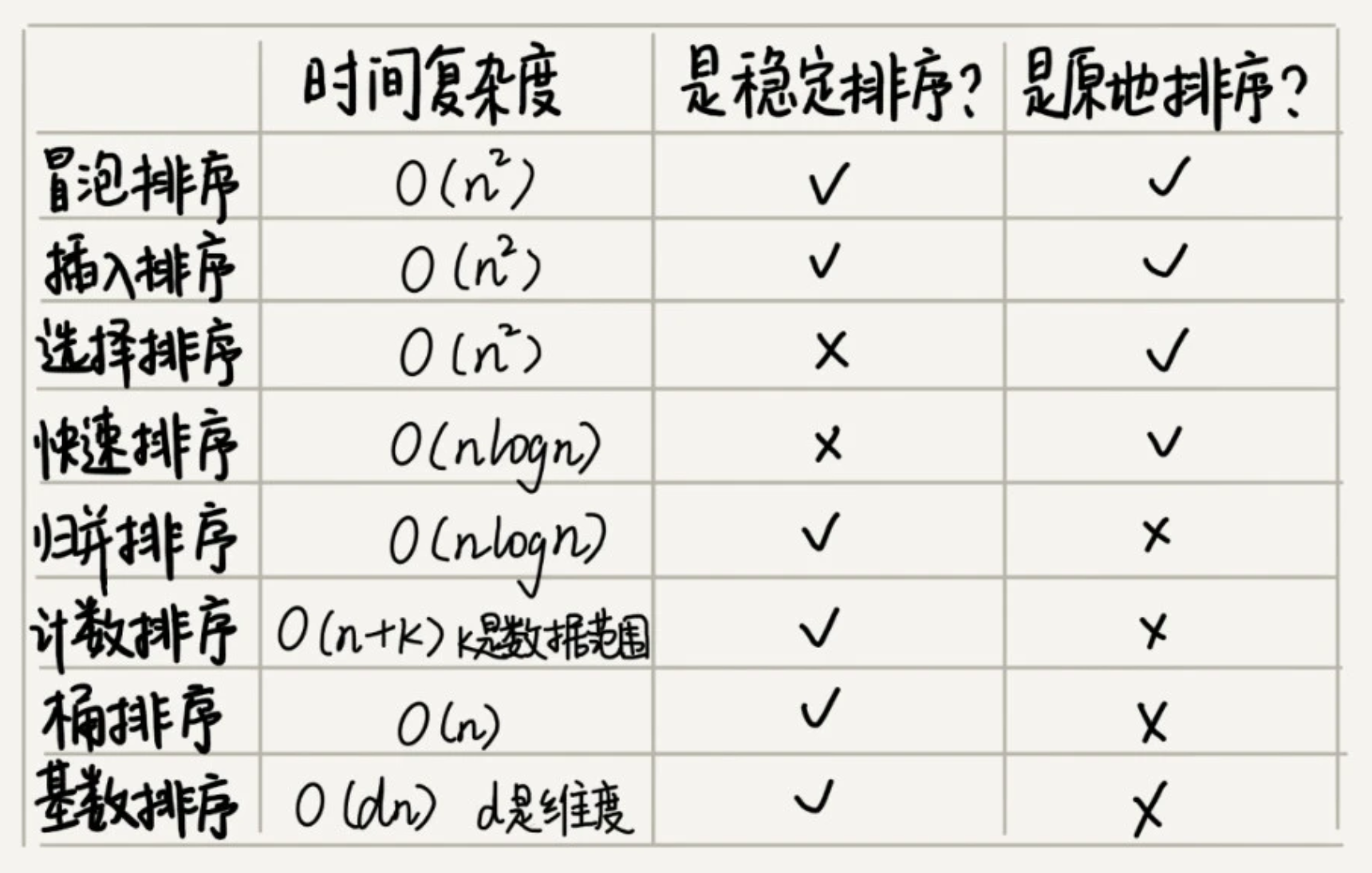
冒泡排序
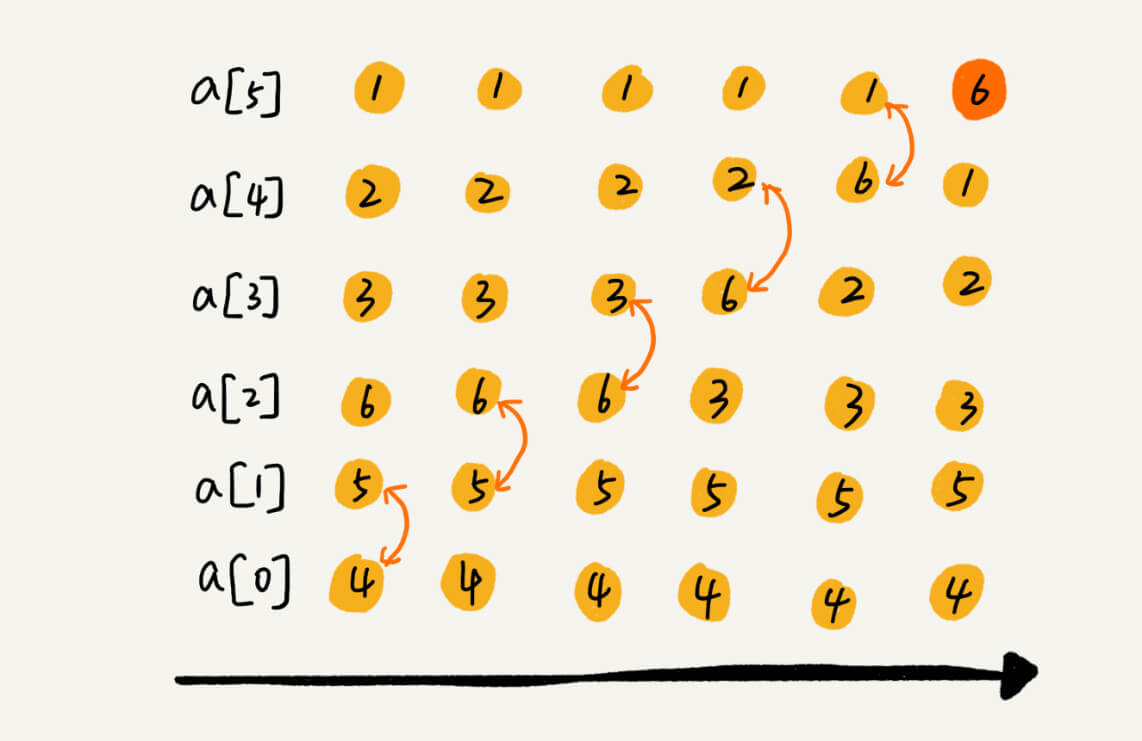
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n-1 次，就完成了 n 个数据的排序工作。

swift实现冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func bubbleSort(_ nums: inout [Int]) {
    for i in 0..<nums.count-1 {
        var flag = true
        for j in 0..<nums.count-1-i {
            if nums[j] > nums[j+1] {
                let temp = nums[j+1]
                nums[j+1] = nums[j]
                nums[j] = temp
                flag = false
            }
        }
        if flag { break }
    }
}

稳定性

在冒泡排序中，只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性，当有相邻的两个元素大小相等的时候，我们不做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序是稳定的排序算法。

空间复杂度

冒泡的过程只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为 O(1)，是一个原地排序算法。

时间复杂度

最好情况下，要排序的数据已经是有序的了，我们只需要进行一次冒泡操作，就可以结束了，所以最好情况时间复杂度是 O(n)。而最坏的情况是，要排序的数据刚好是倒序排列的，我们需要进行 n 次冒泡操作，所以最坏情况时间复杂度为 O(n2)。平均情况时间复杂度也为 O(n2)。

插入排序

插入排序

首先，我们将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束。

冒泡排序和插入排序的时间复杂度都是 O(n2)，都是原地排序算法，为什么插入排序要比冒泡排序更受欢迎呢？
从代码实现上来看，冒泡排序的数据交换要比插入排序的数据移动要复杂，冒泡排序需要 3 个赋值操作，而插入排序只需要 1 个。

swift实现插入排序

1
2
3
4
5
6
7
8
9
10
11
func insertionSort(_ nums: inout [Int]) {
    for i in 1..<nums.count {
        let temp = nums[i]
        var j = i - 1
        while j >= 0 && nums[j] > temp {
            nums[j+1] = nums[j]
            j -= 1
        }
        nums[j+1] = temp
    }
}

稳定性

对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。

空间复杂度

插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是 O(1)，也就是说，这是一个原地排序算法。

时间复杂度

如果要排序的数据已经是有序的，我们并不需要搬移任何数据。如果我们从尾到头在有序数据组里面查找插入位置，每次只需要比较一个数据就能确定插入的位置。所以这种情况下，最好是时间复杂度为 O(n)。注意，这里是从尾到头遍历已经有序的数据。
如果数组是倒序的，每次插入都相当于在数组的第一个位置插入新的数据，所以需要移动大量的数据，所以最坏情况时间复杂度为 O(n2)。
平均情况时间复杂度为O(n2)。

选择排序

选择排序

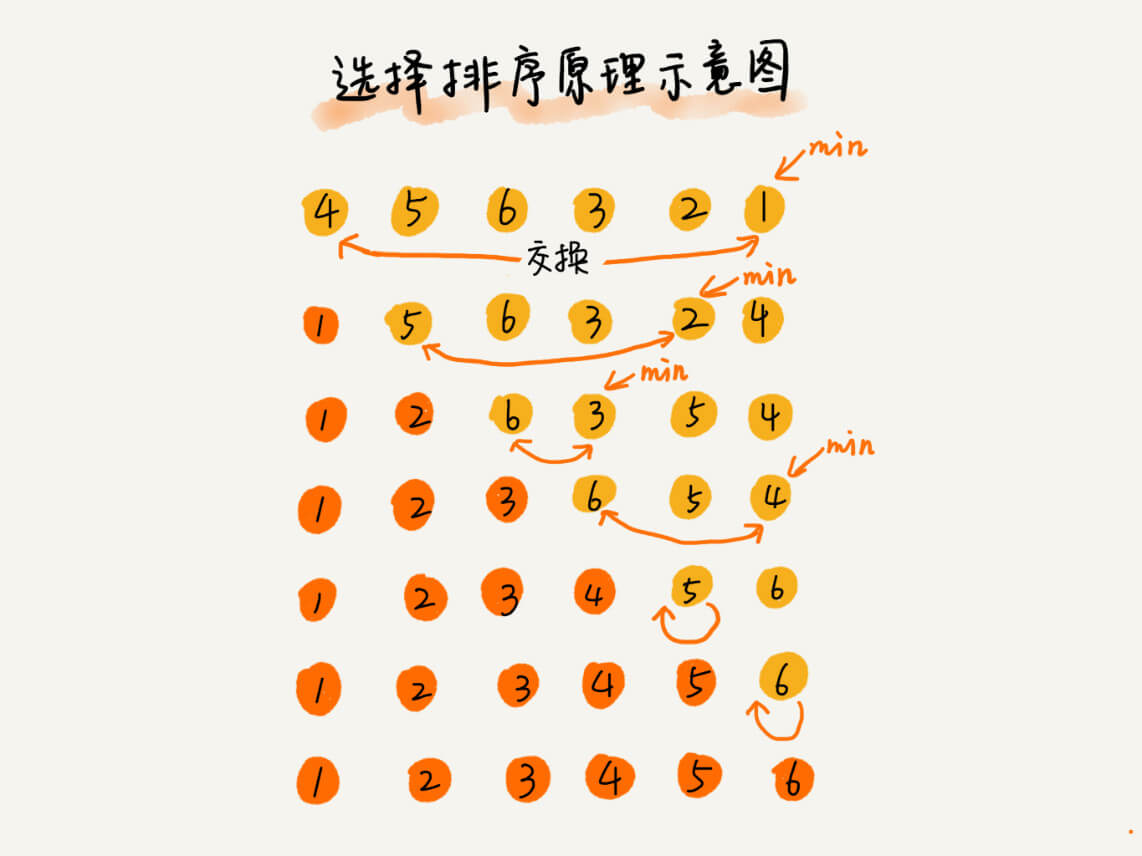
选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

swift实现选择排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//选择排序的交换过程中破坏了稳定性，其不是稳定的排序算法
func selectionSort(_ nums: inout [Int]) {
    for i in 0..<nums.count {
        var j = i
        var min = nums[i]
        var minIndex = j
        while j<nums.count {
            if nums[j]<min {
                min = nums[j]
                minIndex = j
            }
            j += 1
        }
        let temp = nums[i]
        nums[i] = min
        nums[minIndex] = temp
    }
}

稳定性

选择排序是一种不稳定的排序算法，选择排序每次都要找剩余未排序元素中的最小值，并和前面的元素交换位置，这样破坏了稳定性。正是因此，相对于冒泡排序和插入排序，选择排序就稍微逊色了。

空间复杂度

选择排序空间复杂度为 O(1)，是一种原地排序算法。

时间复杂度

选择排序需要 2 次循环遍历，所以最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n2)。

归并排序

归并排序
递归的归并排序

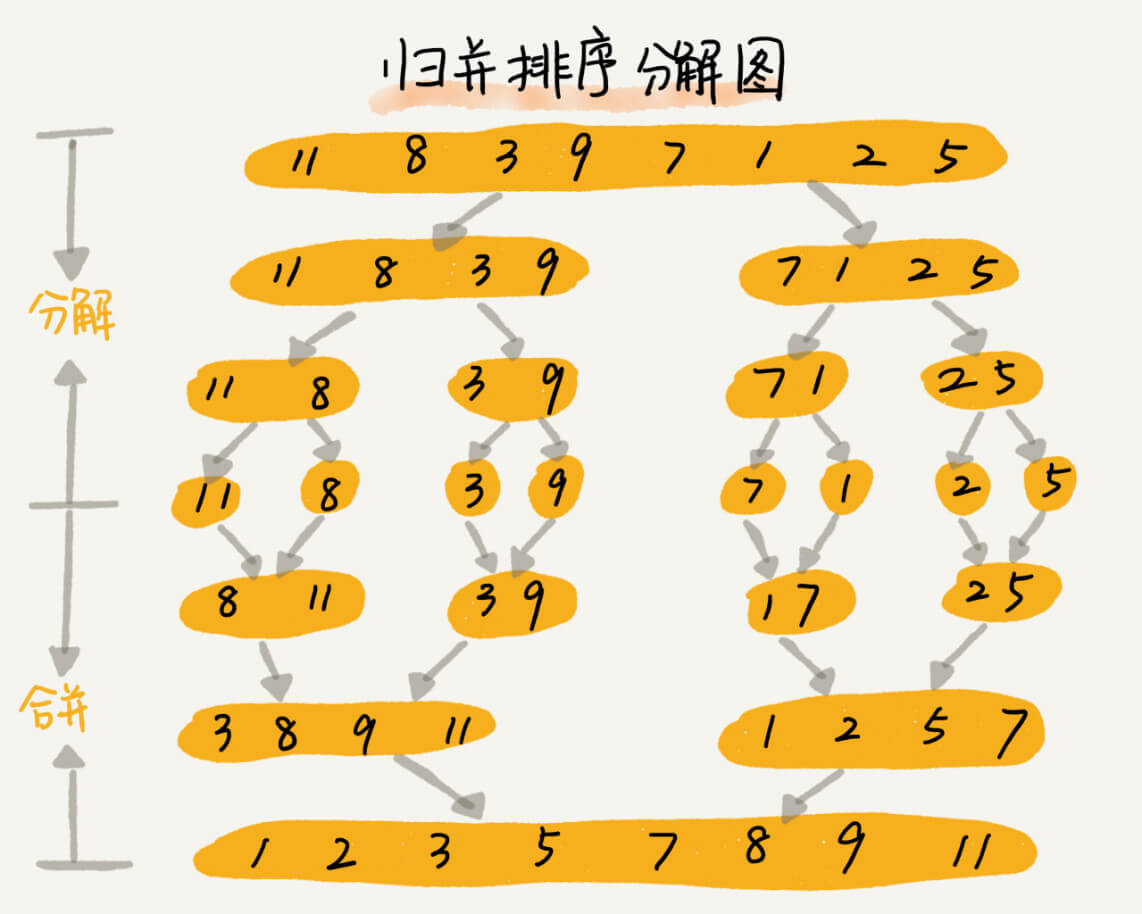
归并排序使用分治思想，先把待排序序列拆分成一个个子序列，直到子序列只有一个元素，停止拆分，然后对每个子序列进行边排序边合并。归并排序的一个缺点是它需要一个临时的“工作”数组，其大小与被排序的数组相同。 它不是原地排序
分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧，这两者并不冲突。

swift实现归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
func mergeSort(_ array: [Int]) -> [Int] {
    guard array.count > 1 else { return array }    
    let middleIndex = array.count / 2              
    let leftArray = mergeSort(Array(array[0..<middleIndex]))             
    let rightArray = mergeSort(Array(array[middleIndex..<array.count]))  
    return merge(leftArray,rightArray)             
}

func merge(_ leftPile: [Int],_ rightPile: [Int]) -> [Int] {
    var leftIndex = 0
    var rightIndex = 0
    var orderedPile = [Int]()
    while leftIndex < leftPile.count && rightIndex < rightPile.count {
        if leftPile[leftIndex] < rightPile[rightIndex] {
            orderedPile.append(leftPile[leftIndex])
            leftIndex += 1
        } else if leftPile[leftIndex] > rightPile[rightIndex] {
            orderedPile.append(rightPile[rightIndex])
            rightIndex += 1
        } else {
            orderedPile.append(leftPile[leftIndex])
            leftIndex += 1
            orderedPile.append(rightPile[rightIndex])
            rightIndex += 1
        }
    }
    while leftIndex < leftPile.count {
        orderedPile.append(leftPile[leftIndex])
        leftIndex += 1
    }
    while rightIndex < rightPile.count {
        orderedPile.append(rightPile[rightIndex])
        rightIndex += 1
    }
    return orderedPile
}

稳定性

在元素拆分的时候，虽然相同元素可能被分到不同的组中，但是合并的时候相同元素相对位置不会发生变化，故稳定。

空间复杂度

需要用到一个数组保存排序结果，也就是合并的时候，需要开辟空间来存储排序结果，在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。

时间复杂度

最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。

快速排序

要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。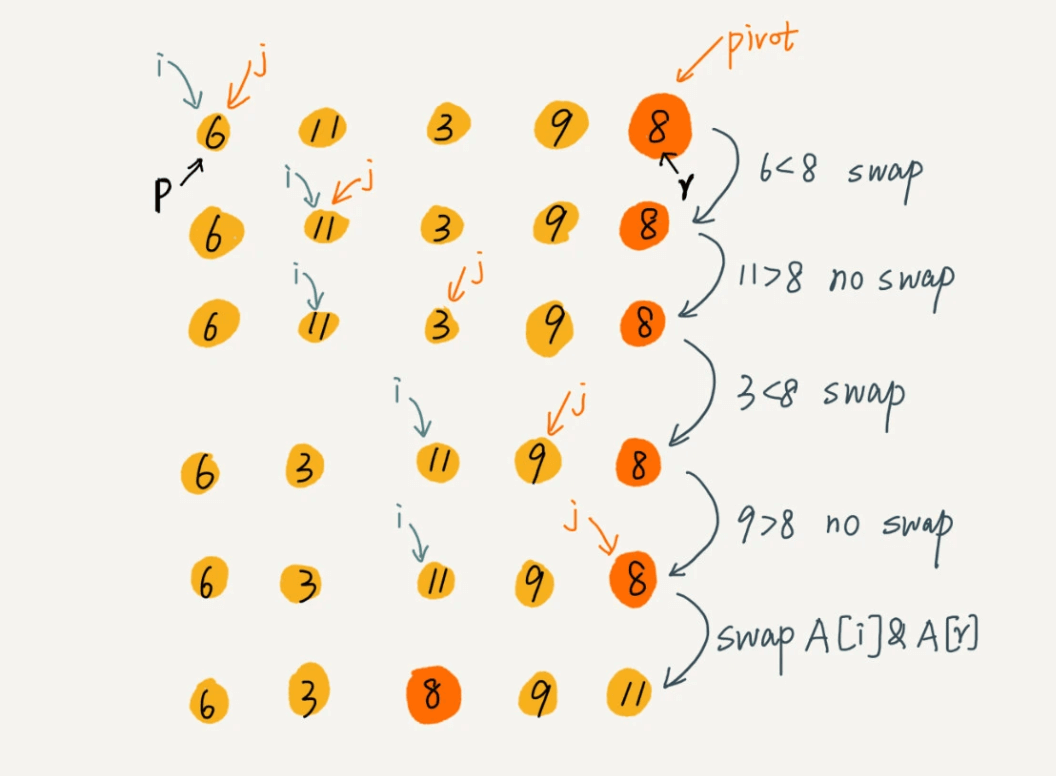
快排分区函数图解

swift实现快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func partition(_ array:inout [Int],_ low:Int,_ high:Int) -> Int {
    let pivot = array[high]//直接选择最后一个数字为分区点
    var i = low
    for j in low..<high {
        if array[j] < pivot {
            let temp = array[j]
            array[j] = array[i]
            array[i] = temp
            i += 1
        }
    }
    array[high] = array[i]
    array[i] = pivot
    return i
 }

func quickSortC(_ array:inout [Int],_ low:Int,_ high:Int) -> Void {
    if low >= high { return }
    
    let index = partition(&array, low, high)
    quickSortC(&array,low,index-1)
    quickSortC(&array,index+1,high)
}
func quickSort(_ array:inout [Int]){
    quickSortC(&array, 0, array.count-1)
}

稳定性

在元素分组的时候，相同元素相对位置可能会发生变化，故不稳定。

空间复杂度

不同实现空间复杂度不太一样，可以实现原地排序，空间复杂度为O(1)。

时间复杂度

与选取的 pivot 值有关系，如果 pivot 值为最大或最小，导致只有一边进行快速排序，时间复杂度为 O(n2) , 如果选择中间的值为 O(nlogn),平均时间复杂度为O(nlogn);

归并排序和快速排序的区别

归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。我们前面讲过，归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。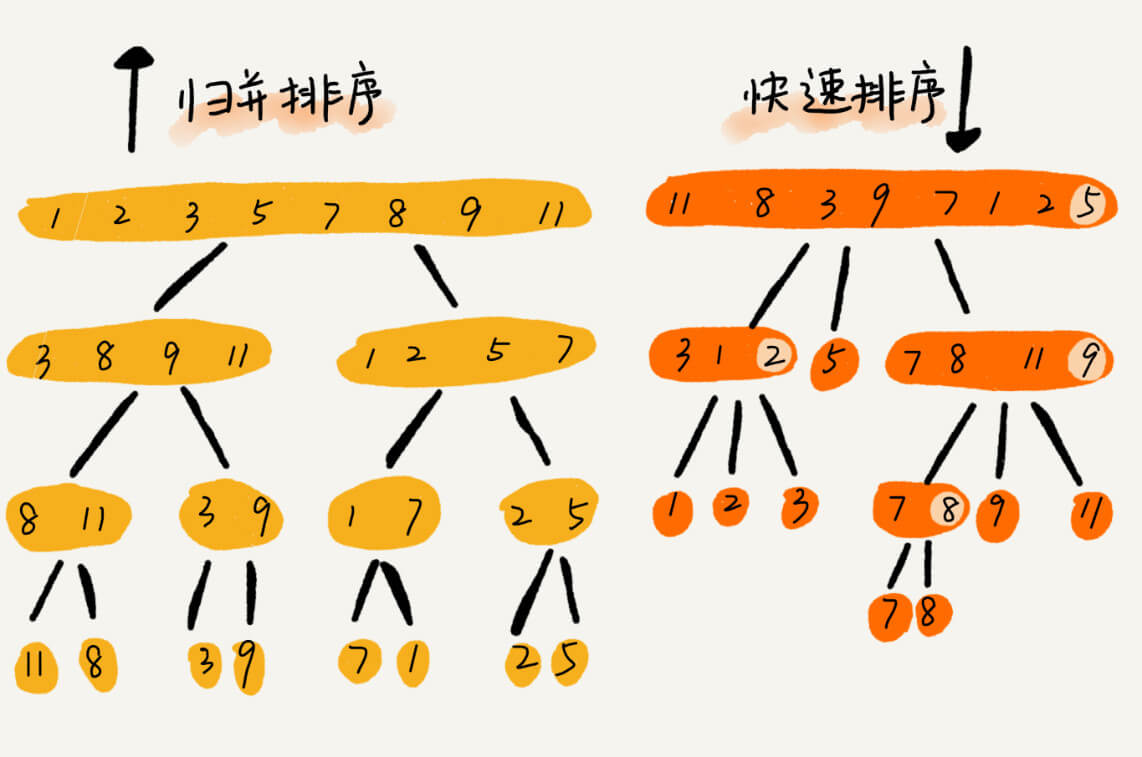
归并快排区别

计数排序

计数排序

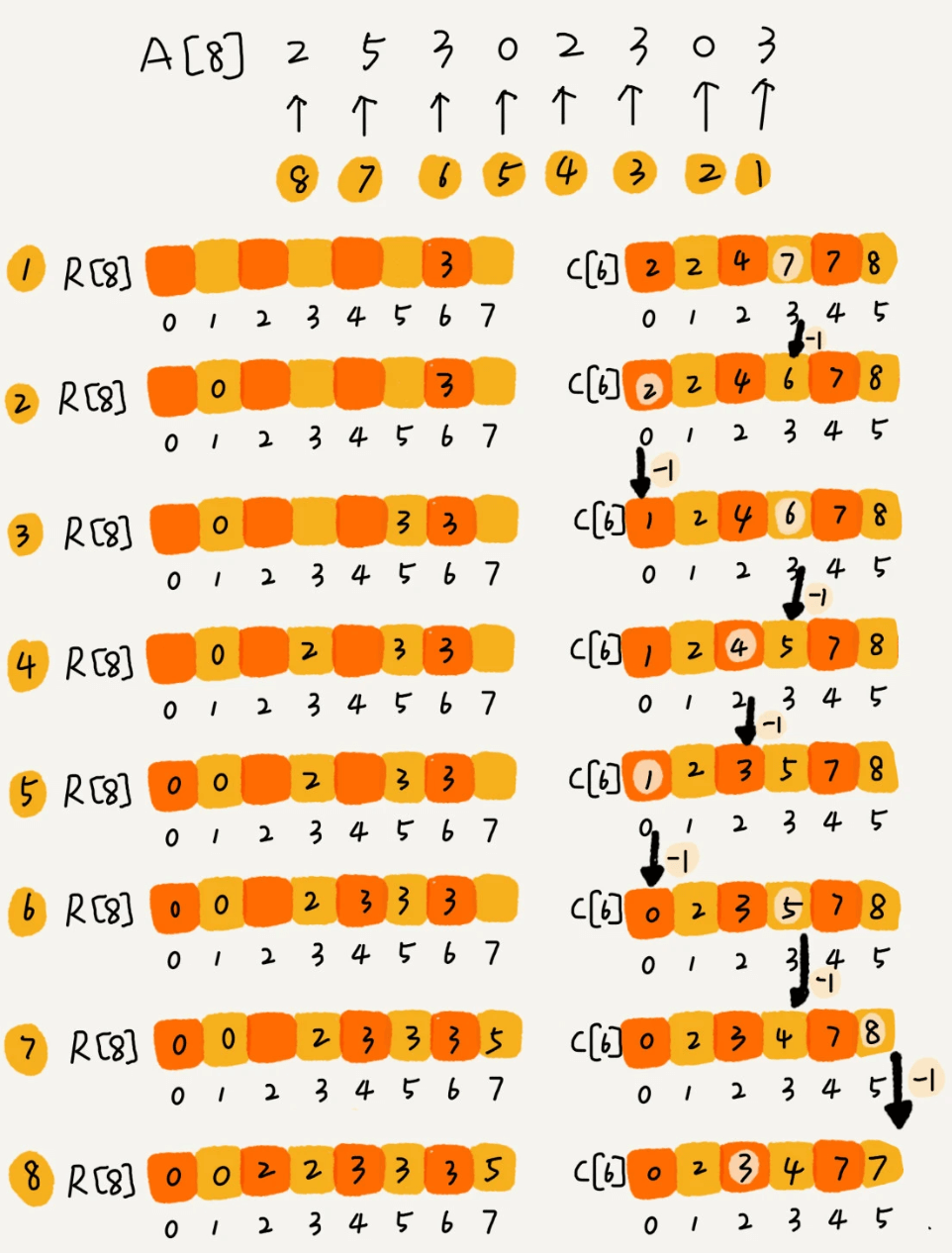
计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。

计数排序的思想是，对每一个输入元素，计算小于它的元素个数，构造辅助数组C，C的长度为k。第一次遍历A后，得到[0,k)区间上每个数出现的次数，将这些次数写入C，然后把C中每个元素变成前面所有元素的累加和，接下来，再次从后向前遍历数组A，根据取出的元素查找C中对应下标的值，再把这个值作为下标找到R中的位置，即是该元素排序后的位置。

swift实现计数排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func countingSort(_ array: [Int]) -> [Int] {
    guard array.count > 1 else { return array }

    let max = array.max() ?? 0
    var countArray = [Int](repeating: 0, count: Int(max + 1)) //其中存储小于或者等于元素值的个数
    for i in array {
        countArray[i] += 1//计算每个元素出现的次数
    }

    for i in 1 ..< countArray.count {
        let sum = countArray[i] + countArray[i - 1]
        countArray[i] = sum//算出小于等于此元素值的个数
    }
    
    var sortedArray = [Int](repeating: 0, count: array.count)
    for i in array {
        countArray[i] -= 1
        sortedArray[countArray[i]] = i
    }
    return sortedArray
}

稳定性

空间复杂度

该算法使用长度为n + 1和n的数组，因此所需的总空间为O(2n)

时间复杂度

第一次遍历A并计算C所花时间是O(n)，C累加所花时间是O(k)，再次遍历A并给R赋值所花时间是O(n)，因此，总时间为O(k + n)。在实际中，当k=O(n)时，我们一般会采用计数排序，这时的运行时间为O(n)。